|
Thomas Bugge: De første Grunde til den rene eller abstrakte Mathematik. Tredje og sidste Deel. Den oekonomiske og den militaire Landmaaling. Kiøbenhavn 1814.
Download dette dokument i Word-format.
Download dette dokument i
pdf-format.
§ .76.
Tab.23.
Fig.63 og Fig.64
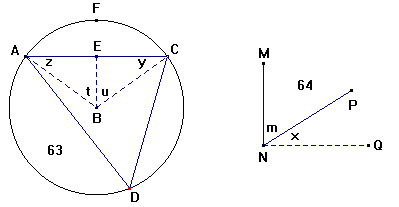
Naar der gives en ret Linie AC, da at indskrive den
saaledes i en Cirkel, at naar AC er en Chorde 1) og Grundlinien til
et Segment2) ACD, Vinkelen i Segmentet eller ved Peripherien D
bliver saa stor som en given Vinkel m, eller at indskrive den givne Linie AC i
en saadan Cirkel, at Buen AFC, hvortil AC er Chorden, er dobbelt saa stor som en
given Vinkel m.
1. Paa Linien MN af den givne Vinkel m opreises en
Perpendikular 3) NQ (§.123 Geom.4) ); da er
m + x = 90o (§.11 Geom.5)); og x = 90o
- m, eller x er Komplementet til m (§.3 Trig.6)).
2. Ved Enden C af den givne Linie AC aftegnes Vinkelen y = x;
ligeledes ved A aftegnes z = x (§.20 Teom. 7)).
3. Disse Linier forlænges, indtil de skiære hinanden i B.
4. Af B, som Center, med Radius AB eller BC beskrives en
Cirkel (§.55 Geom.8) ).
5. Naar man nu fra A og B til ethvert Punkt D i denne Cirkels
Peripherie drager Linien AD og CD, saa er Vinkelen D = m: og Buen AFC = 2m.
Beviis. Man deler AC i tvende lige Parter i E, og drager BE,
saa er Triangelen BCE retvinklet ved E (§.107 Geom.9) );
altsaa u + y = 90o (§.67 Geom.10) ) = m + x; man
fradrager y = x, saa er u = m (§.6 Arith.11)). Paa samme
Maade bevises i Triangelen AEB, at t = m; altsaa u + t = 2m; og ½u + ½t = m
(§.6 Num.4 Arith. 11)); men u + t er en Center - Vinkel og
Halvparten af Vinkelen ved Peripherien eller ½u + ½t = D (§.121 Geom.12));
altsaa m = D. Fremdeles da t + u = 2D, men t + u = AFC (§.28 Geom.13));
saa er 2D = AFC; eller den Bue AFC, hvortil AC er Chorden, er dobbelt saa stor
som den givne Vinkel m.
§ 77
Tab.23.
Fig.65
og Fig.66.
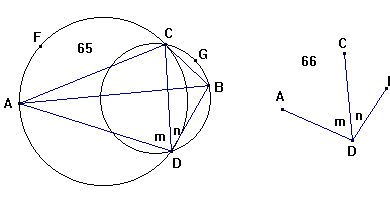
Naar der gives trende Objekter paa Marken, A, B og C, som
danne en given Triangel, eller naar Objekterne A, B og C rigtigen ere aflagte i
Kartet, og Siderne AB, BC, og AC ere bekiendte, og man desuden paa et tredie
Sted D med Maalebordet tager Vinklerne mellem disse Objekter, nemlig imellem A
og C = m, og imellem C og B = n, da paa Kartet uden videre Maaling at bestemme
Punktet D, og finde DA, DC, og DB.
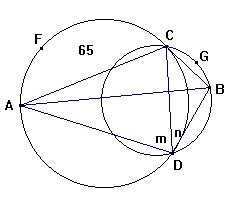
1. Opløsning. 14)
1. Paa den givne Side AC aftegner man en Cirkelbue AFC,
som er dobbelt saa stor som den givne Vinkel m imellem Objekterne A og C
(§.76).
2. Paa den givne Side CB aftegner man en Bue CGB, hvilken er
dobbelt saa stor som den givne Vinkel n imellem Objekterne C og B.
3. Disse Cirkler skiære hinanden udi D, hvilket bliver
Stationens Sted paa Bordet, og AD, DC og DB Stationens Afstand fra de givne
Objekter A, B og C.
Beviis. Efter Betingelsen er Siden AC eller Afstanden imellem
Objekterne A og C seet i Stationen D under Vinkelen m; og da alle Vinkler i
samme Cirkel-Segment ere lige store (§.122 Geom.15)); saa
maae Stationen D falde et Sted i Peripherien af Cirkelen AFCD; ligeledes er
Siden BC seet under Vinkelen n fra samme Station D; altsaa maae Stationen D
falde et Sted i peripherien af Cirkelen CGBD; men da disse tvende Cirkler
skiære hinanden udi D, saa er D Stationens Sted paa Maalebordet, og der er ei
noget andet Punkt end Punktet D, fra hvilket AC kan sees under Vinkelen m og
tillige BC under n, og følgelig bliver og AD, CD, og BD Stationens rette
Afstand fra Objekterne A, B, og C.
2. Opløsning.
Tab.23
Fig.69
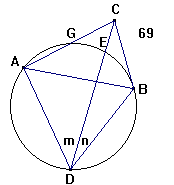
1. Den store Side AB indskriver man i en Cirkel AEBD,
saaledes at Buen AEB er dobbelt saa stor som Summen af begge de observerte
Vinkler ADB = m + n (§.76).
2. Man tager Buen AGE til dobbelt saa mange Grader som
Vinkelen ADC = m; hvoraf da følger, at BE har dobbelt saa mange Grader som n.
3. Man drager Linien CED, saa er D Stations- Punktets Sted
paa Bordet; thi AGE = 2m; og EB = 2n; altsaa er m = ½ ACE den Vinkel, under
hvilken AC er seet, og n = ½ EB er den Vinkel, under hvilken CB er seet fra
Stationen D.
3. Opløsning.
Tab.23
Fig. 67
og Fig.68
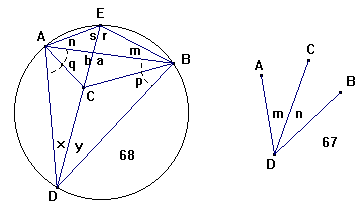
Hvis man antager, at Spidsen af Trianglen C vender mod
Stationen D.
1. Paa AB og ved Punktet B aftegnes Vinkelen ABE = m (§.30
Geom. 16)); og paa samme Linie ved A aftegnes Vinkelen BAE =
n, saa at den Vinkel m, som blev observeret imellem A og C, aftegnes ved B, og
den Vinkel n, som er bekiendt imellem C og B, aftegnes ved A.
2. Man drager Linien CE, hvorved fremkommer Vinklerne s og r.
3. Man aftegner Vinkelen ABD eller p = s; og hvor Linien BD
skiærer den forlængede EC, bliver det søgte Punkt D paa Kartet.
4. Til bekræftelse kan man aftegne Vinkelen BAD eller r = q,
hvis Linie AD skal give samme Punkt D paa Kartet.
Beviis. DAa er en Triangel, i hvilken den udvendige Vinkel a
= q + x eller de tvende indvendige, (§.66 Geom.); ligeledes i Triangel
aDB er b = p + y: og ved at lægge sammen a + b = 180 (§.31 Geom. 17)
) = q + p + x + y: men q = r efter Konstruktionen; altsaa r + p + x + y = 180o;
men i Triangel DEB er r + m + p + y = 180o
(§.66 Geom. 18)); følgelig r + p + x + y = r + m + p + y,
naar man nu paa begge Sider fradrager r + p + y, saa bliver x = m. Paa samme Maade bevises, at n = y; hvoraf da
følger, at Punktet D paa Kartet er det Punkt, under hvilket den givne Vinkel m
= ADC, og Objekterne C og B under Vinkelen n = CDB; og AD og DB maae støde
sammen i et Punkt D. 19)
4. Opløsning.
Tab. 24
Fig. 70
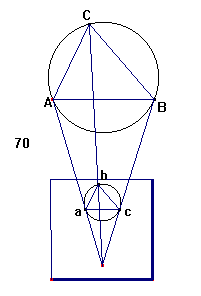
1. Da de trende Objekters Afstand antages at være
bekiendt, eller man allerede har anlagt i Kartet disse Punkter A, B, og C; saa
er paa Kartet den mindre Triangel abc – ª
ABC paa Marken.
2. Denne Triangel abc indskriver man i en Cirkel (§.111
Geom.20)).
3. Man opstiller Maalebordet i D paa et Stykke Olie-Papiir,
som sættes til Bordet med Mund-liim, Naale eller paa anden Maade, tager
Sigterne til de trende Objekter A, C, og B; og derefter giøres det løst.
4. Man lægger og bevæger det oliede Papiir saaledes paa
Kartet, at Sigtelinierne berøre Cirkelen, og at Da, Dc og Db gaae igiennem
Punkterne a, b og c.
5. I denne Stilling holdes Olie-Papiret fast og man
giennemprikker D med en Kopiernaal, saa bliver D Stationens Sted paa Bordet, og
aD, cD og bD Objekternes Afstand til Stationen D efter Kartets Maalestok.
§ 78
Flere Opløsninger deels geometriske, deels
trigonometriske, deels algebraiske paa dette problem kan findes ……
…. Den her givne Opløsning afhandler ikkun det vigtigste og sædvanligst
forekommende Tilfælde, at det givne Punkt D, som blot ved Sigter skal bestemmes
af trende andre A, B og C, som danne en given Triangel, ligger uden for
Trianglen, og altsaa hverken inden i den eller i Linie med nogen af Siderne.
Ligeledes naar der gives trende Punkter i en ret Linie, A, C og B, og man fra et
Sted D maaler Vinklerne ADC og CDB, kan man og bestemme Stedet D. Disse trende
Problemers Opløsninger forstaaes let af det, som her er forklaret om det ene
Tilfælde, og man finder dem og hos adskillige af ovenmeldte Forfattere.
Tab.23
Fig. 65
Dette Problem kan anvendes ved adskillige Leiligheder i
Landmaaling; saasom om en Søe paa den ene halve Deel var bevoren med stor og
tæt Skov, men den anden halve Deel var aaben og frie, da kunde man ved
brækkede Linier efter Søens Omkreds og ved Perpendikularer fra disse
Grundlinier opmaale den aabne Søekant (§.65). Man opreiser da Signaler i
Stationerne, og andre fra de brækkede Linier nøiagtigen bestemte og høit
beliggende Steder. Man gaaer da til den med Skov bevorne Søekant, og opleder
saadanne Steder D, fra hvilke trende af de paa den anden Side bestemte Punkter
A, B og C kan sees; der opstilles Maalebordet, og Sigter tages til disse
Signaler, nemlig ADC og CDB, og heraf bestemmer og anlægger man Punktet D paa
Kartet (§.77). Jo flere saadanne Punkter man kan finde, desto nøiagtigere
bliver den med Skov bevorne Søekant aflagt; undertiden kan det og blive mueligt,
at maale Linier mellem disse Punkter, og bestemme de imellem dem værende Bugter
ved Perpendikularer. Paa papiret synes denne Maade meget simpel og let; men den
har dog mange praktiske Vanskeligheder, af hvilke den vigtigste er, at man paa
den med Skov bevorne Side af Søen ei let kan finde Stederne igien, hvor
Signalerne ere udsatte; og dersom man skulle tage det ene for det andet, da blev
Punkterne paa Kartet meget urigtige, efterdi de bleve anlagte efter en ganske
urigtig Grundtriangel. Problemets Opløsning udfordrer temmelig vidtløftige
Konstruktioner og Aftegninger af flere Linier og Vinkler (§.77); og om paa
enhver Vinkel og Linie ikkun feiles saa meget, som det fineste Punkt og den
fineste Linie udgiør (og for en saa liden Feil kan man aldrig fritage nogen
Linies eller Vinkels Afsætning), saa vil disse uundgaaelige smaae Feil
tilsammentagne dog kunde forandre den rette Beliggenhed af Punktet D paa Kartet.
Af den Aarsag bør man i den speciale Landmaaling ei anvende dette Problem uden
i de yderste Nødvendigheds Tilfælde, naar det ei er mueligt at bestemme
Punktet D enten ved Maal eller Sigte (§.58-59), eller ved tvende Sigter fra
afstukne og opmaalte Grundlinier (§.60), hvilke
Metoder ere meget mere
nøiagtige og paalidelige.
_________________________________________________________________________
Noter:
- Chorde: Et linjestykke der forbinder to punkter på en cirkelperiferi.
- Segment: afsnit, fx en cirkelbue og den tilsvarende korde.
- Perpendikular: En linje der står vinkelret på en anden linje.
- §123Geom:
Fra Enden A af en Linie AB at opreise AD perpendikular til AB.
1. Man vælger sig et Punkt C, med en Passeraabning CA beskriver man en Bue
større end en
Halvcirkel, som skiærer den givne Linie i B.
2. Man drager Linien BC, og forlænger den, indtil den skiærer Cirkelen i D.
3. Fra D til A drages Linien AD, hvilken er perpendikular til AB, efterdi BAD er
en Halvcirkel,
og A = R (§.122 Num.4); altsaa AD perpendikular til AB (§.11).
- § 11 Geom:
….Naar en linie DC er perpendikular til AB….saa er de jevnsides Vinkler
lige store, eller ACD = DCB…..
- § 3 Trig: …..Af tvende Buer AB og BG, eller af tvende Vinkler x og y,
hvilke tilsammen udgiøre 900, siges den ene at være den andens
Complement; saaledes er y Complementet til x……..
- § 20 Geom: Ved et givet Punkt E i en given Linie EF, at aftegne en Vinkel E
lige stor med en given Vinkel B eller ABC. …..
- § 55 Geom: Naar i en Triangel ABC Vinklerne ved Grundlinien ere lige store,
A = B, saa er Trianglen ligebenet AC = CB. ……
- § 107 Geom: En Diameter DE, som skierer Chorden AB i tvende lige Parter, AF
= FB, er perpendikular til Chorden AB. …..
- § 67 Geom: … Naar der i en Triangel ABC gives Tvende Vinkler A og B, saa
findes den tredie Vinkel C ved at drage de tvende givne Vinklers Summa fra
tvende rette Vinkler. …..
- § 6 Arith: Naar lige store Størrelser forøges eller formindskes lige
meget og paa samme Maade, saa er det Udkomne lige.
- § 121 Geom: Vinkelen ved Centeret ACB er dobbelt saa stor som Vinklen ved
Peripherien ADB, naar de begge staae paa samme Bue AB. ……
- § 28 Geom:
Henvisningen er uklar.
- fra ordbog over det danske sprog: 5) nu især regn. Og mat.forklaring,
opklaring, tydning, udregning, løsning.
- § 122: Alle Vinkler i samme Cirkel-Segment AFEDB ere lige store; (fig124)…..
- § 30 Geom: Ved et givet Punkt E i en given Linie EF, at aftegne en Vinkel E
lige stor med en given Vinkel B eller ABC. …..
- § 31 Geom: Naar paa en Linie AB staaer en anden Linie CD, saa ere begge de
jevnsides Vinkler ACD og DCB tilsammentagne tvende rete Vinkler eller 180
Grader…….
- § 66 Geom: Naar i enhver Triangel ABC den ene Side AB forlænges til D, er
den udvendige Vinkel DBC saa stor som de tvende indvendige og modstaaende
Vinkler A + C, og alle Vinkler tilsammentagne er saa stor som tvende rette A +
C + y = 2R…….
- Bemærk at, I beviset gøres der ikke rede for at den linie der omtales i
punkt 4 skærer i D
- § 111 Geom: Igiennem trende givne Punkter A, B og C, hvilke ei ligge i
samme rette Linie, at beskrive en cirkel…….
|





